قانون محيط متوازي الأضلاع

متوازي الأضلاع هو شكل من الأشكال الهندسية، وهو ذو أهمية كبيرة في الرياضيات والهندسة، حيث يستخدم في العديد من المجالات مثل الهندسة المعمارية والهندسة الميكانيكية وعلوم الحاسوب، وذلك بفضل شكله الهندسي المميز وخصائصه الفريدة التي يتم دراستها بعمق في الرياضيات الهندسية.

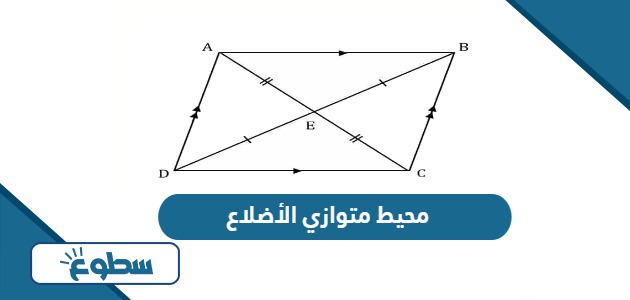
قانون محيط متوازي الأضلاع

محيط متوازي الأضلاع يمكن حسابه ببساطة عن طريق جمع جميع أطوال أضلاعه، أو جمع أطوال الضلعين المتقابلين، أي إذا كان لدينا متوازي الأضلاع، فإن محيطه يكون مجموع طول الضلعين مضروبًا في 2، لذا، محيط متوازي الأضلاع = (ضلع × 2) + (الضلع الآخر × 2)، وبالرموز يكن:^[1]

• محيط متوازي الأضلاع = (a + b) × 2.
• محيط متوازي الأضلاع = (2a + 2b)

حيث:

• a: هو طول ضلع متوازي الأضلاع.
• b: هو عرض متوازي الأضلاع، أي طول الضلع الآخر.

اقرأ أيضًا: خصائص متوازي الأضلاع | شكل متوازي الاضلاع بالصور | قانون مساحة متوازي الاضلاع