قانون مساحة متوازي الاضلاع
–تاريخ النشر:
جدول المحتويات
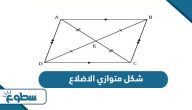
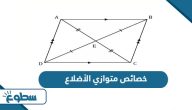
يعدُّ متوازي الأضلاع أحد الأشكال الهندسية البسيطة في عالم الرياضيات والهندسة، حيث يتميز بأضلاع متوازية متساوية الطول، كما أن زواياه متساوية القياس، مما يمنحه شكلاً متناغمًا وجميلاً يثير اهتمام المتعلمين والباحثين على حد سواء، لذلك يستخدم في العديد من التطبيقات الهندسية والرياضية.
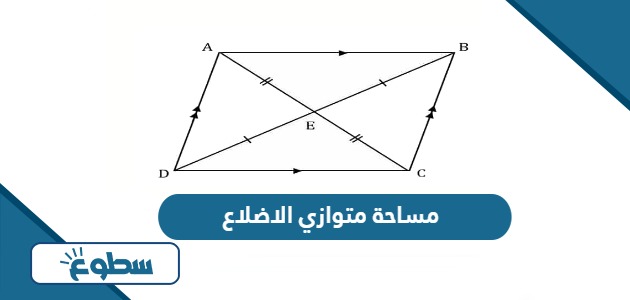
قانون مساحة متوازي الاضلاع
فيما يلي قوانين حساب مساحة متوازي الأضلاع في عدة حالات:[1]
| مساحة متوازي الأضلاع | الشرح | قانون مساحة متوازي الأضلاع بالرموز |
| مساحة متوازي الأضلاع حسب معرفة طول القاعدة والارتفاع | مساحة متوازي الأضلاع يمكن حسابها باستخدام القاعدة مضروبة في الارتفاع، حيث تُعبر القاعدة عن طول إحدى القواعد في متوازي الأضلاع، ويكون الارتفاع العمودي للمتوازي، لذا، مساحة متوازي الأضلاع تساوي القاعدة في الارتفاع. |
حيث:
|
| مساحة متوازي الأضلاع حسب معرفة طول القطرين وزاوية بينهما | مساحة متوازي الأضلاع يمكن حسابها عند معرفة طول أقطار متوازي الأضلاع، وقياس الزاوية المحصورة بينهم، حيث تكون مساحة متوازي الأضلاع في هذه الحالة هي حاصل جداء طول القطرين، بنصف جيب أي sin الزاوية المحصورة بينهم. |
حيث:
|
| مساحة متوازي الأضلاع حسب معرفة طول ضلعين وزاوية بينهما | مساحة متوازي الأضلاع يمكن حسابها عند معرفة طول أقطار متوازي الأضلاع، وقياس الزاوية المحصورة بينهم، حيث تكون مساحة متوازي الأضلاع في هذه الحالة هي حاصل جداء طول القطرين، بنصف جيب أي sin الزاوية المحصورة بينهم. |
حيث:
|
اقرأ أيضًا: خصائص متوازي الأضلاع | قانون محيط متوازي الأضلاع | شكل متوازي الاضلاع بالصور
المراجع
- toppr.com , Area and perimeter of a parallelogram , 2024-11-24